这道题我个人认为非常经典，在评论区看了大神的代码，自己5分钟就手写了一遍，问题的难点从来都不是代码，而是在思路。
当我拿到这个题目时想分析有哪几种异常情况，分析发现根据这些异常情况判断比较复杂，很难较全面的判断。
比如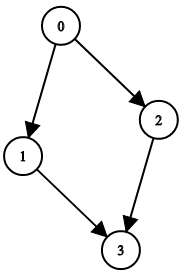

Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
Output: false

我开始以为leftChild和rightChild中不能有重复元素，但问题远比这种情况复杂。

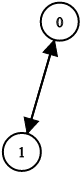
Input: n = 2, leftChild = [1,0], rightChild = [-1,-1]
Output: false

这种场景也没有重复，但是存在多个root结点，因此也不合法。
正确的解法分为两步：
1.找到唯一root(如果不唯一 false)
2.DFS或BFS统计结点个数是否与传入参数一致，如果不是合法二叉树，个数必然不一致。
使用这种方法问题就变得非常非常简单。

class Solution {
public:
    bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {
        vector<int> inDegree(n,0);
        int root = -1;
        //遍历左右子树，更新所有结点入度
        for(int i = 0;i < leftChild.size();i++)
        {
            if(leftChild[i] != -1 && inDegree[leftChild[i]]++ == 1)
                return false;
        }
    
        for(int i = 0;i < rightChild.size();i++)
        {
            if(rightChild[i] != -1 && inDegree[rightChild[i]]++ == 1)
                return false;
        }
            
        for(int i = 0;i < inDegree.size();i++)
        {
            if(!inDegree[i])
            {
                if(root == -1)
                    root = i;
                else
                    return false;
            }
        }
        
        if(root == -1) return false;
        
        return count_node(leftChild,rightChild,root) == n;
    }
private:
    int count_node(vector<int>& l, vector<int>& r,int root) {
        if(root == -1) return 0;
        
        return 1 + count_node(l,r,l[root]) + count_node(l,r,r[root]);
    }
};