46.Permutations
一口气刷了3道简单题目，正当得意忘形的时候遇到了一道求全排列的题，竟然一时间不知道如何下手。
由于恰好看algorithm中有实现next_permutation，因此直接使用stl中的现有实现：

方法一：

next_permutation

class Solution {
public:
    vector<vector<int> > permute(vector<int> &num) {
        vector<vector<int> > ans;
        sort(num.begin(), num.end());
        
        ans.push_back(num);
        
        while(next_permutation(num.begin(), num.end()))
            ans.push_back(num);
        return ans;
}
};

运行结果：
Runtime: 8 ms, faster than 98.88% of C++ online submissions for Permutations.
Memory Usage: 9.1 MB, less than 100.00% of C++ online submissions for Permutations.

由此可见运行速度相对较快比98.88%提交快,内存占用更是击败100%。

如果是在面试的时候，面试官问你如何求全排列，这个时候你抛出来方法一只能说明你熟悉这个算法，但面试官的真正意图肯定是希望你自己实现。

方法二：

递归实现

class Solution {
public:
    vector<vector<int> > permute(vector<int> &num) {
        vector<vector<int> > result;
        permuteRecursive(num, 0, result);
        
        return result;
}

private:
    void permuteRecursive(vector<int> &num, int begin, vector<vector<int> > &result)
    {
        if(begin >= num.size())
        {
            result.push_back(num);
            return;
        }
        
        for(int i = begin;i < num.size();i++)
        {
            swap(num[i],num[begin]);
            permuteRecursive(num, begin + 1, result);
            swap(num[i],num[begin]);    
        }
        
    }
};

运行结果：
Runtime: 12 ms, faster than 71.01% of C++ online submissions for Permutations.
Memory Usage: 9.2 MB, less than 94.03% of C++ online submissions for Permutations.
我们可以看到我们的递归实现版本效率比algorithm中的实现运行速度略慢。

这个实现用递归比较难理清楚，原因是递归调用里面有for循环。递归的难点是将问题的规模变小和终止条件。

一个完整的程序，可以编译后调试查看原理。

#include <iostream>
#include <vector>
using namespace std;
    
// permute num[begin..end]
// invariant: num[0..begin-1] have been fixed/permuted
void permuteRecursive(vector<int> &num, int begin, vector<vector<int> > &result)    
{
    if (begin >= num.size()) {
        // one permutation instance
        result.push_back(num);
        return;
    }
    
    for (int i = begin; i < num.size(); i++) {
        swap(num[begin], num[i]);
        permuteRecursive(num, begin + 1, result);
        // reset
        swap(num[begin], num[i]);
    }
}

vector<vector<int> > permute(vector<int> &num) 
{
    vector<vector<int> > result;
    
    permuteRecursive(num, 0, result);
    return result;
}

int main()
{
    vector <int> nums{1,2,3};
    vector<vector<int>> ans = permute(nums);

    for(auto iter = ans.begin();iter != ans.end();iter++)
    {
        for(auto it = (*iter).begin();it != (*iter).end();it++)
        {
            cout << *it <<" ";
        }
        cout << "\n";
    }
    return 0;
}

实现原理参考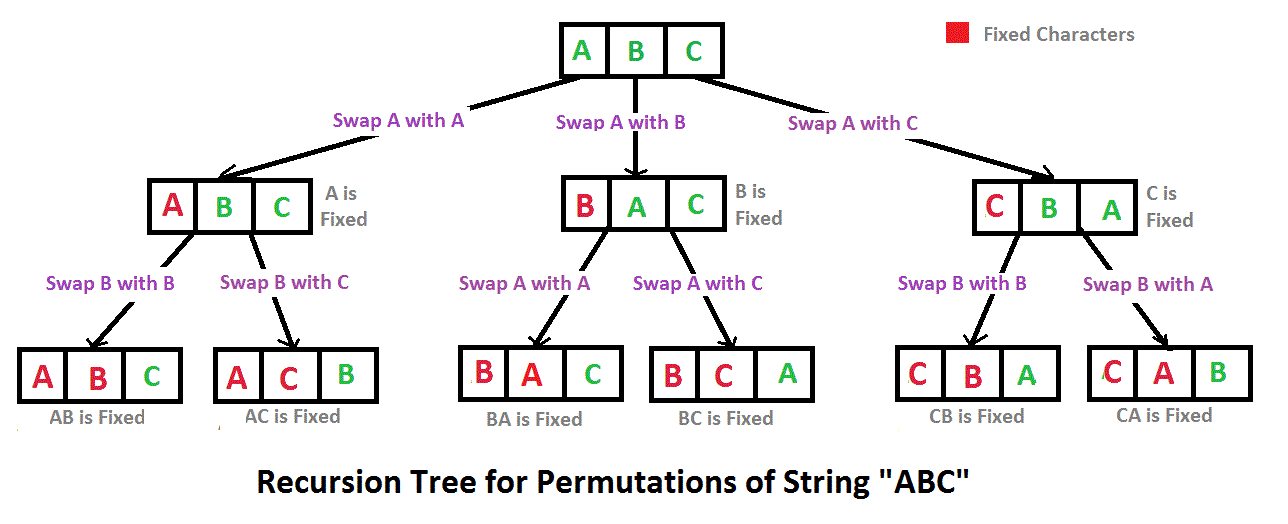,完整文章参考解决全排列问题
我们只看外层调用，num的值调用permuteRecursive前是{1,2,3},然后初始交换i == begin == 0,此时不交换，执行swap后，num的值依旧是{1,2,3}.
执行一次permuteRecursive后，我们看到result中已经加入了{1,2,3}和{1,3,2}.

然后下一次循环中交换下标0和1中的值，此时num的值是{2,1,3}.
执行一次permuteRecursive后，我们看到result中已经加入了{2,1,3}和{2,3,1}.
循环结尾会将num的值复原，保证for循环每次调用num的值都是{1,2,3}

下一次循环中交换下标0和2中的值，此时num的值是{3,2,1}.
执行一次permuteRecursive后，我们看到result中已经加入了{3,2,1}和{3,1,2}.
循环结尾会将num的值复原，保证for循环每次调用num的值都是{1,2,3}
这样我们就分析完了最上层的那一层调用，然后再继续分析第二层同样的道理。
递归的终止条件是begin >= num.size()，此时将整个vector插入result即可。函数走到这里已经包含了完整的一个排列。

调试到一半发现可以将递归终止条件修改为begin >= num.size() - 1，完整代码如下：

class Solution {
public:
    vector<vector<int> > permute(vector<int> &num) {
        vector<vector<int> > result;
        permuteRecursive(num, 0, result);
        
        return result;
}

private:
    void permuteRecursive(vector<int> &num, int begin, vector<vector<int> > &result)
    {
        if(begin >= num.size() - 1)
        {
            result.push_back(num);
            return;
        }
        
        for(int i = begin;i < num.size();i++)
        {
            swap(num[i],num[begin]);
            permuteRecursive(num, begin + 1, result);
            swap(num[i],num[begin]);    
        }
        
    }
};

我在讨论区的留言permutations dissuss