本文是算法概论读书笔记,算法概论这本书在豆瓣评分高达9分,在收到学弟寄来的这本书我随手翻了几页就被书中所述内容所吸引,因此本文持续记录书中对于我来说比较有意思又或者我之前理解不深刻或错误的地方。
序言
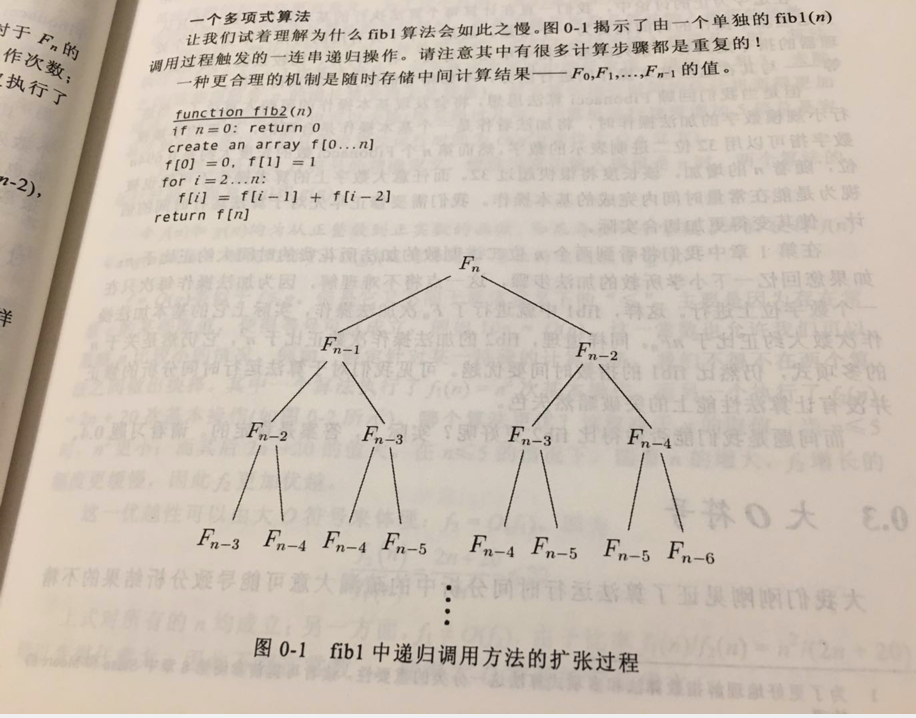
序言部分从费波那奇数列介绍开始,引入费波那奇数列的递归实现,接着分析递归实现算法慢的原因,因为很多求解步骤都是重复的。一种更合理的机制是随时存储中间计算结果。
C语言实现:
#include <stdio.h>
int Fibonacci(int n)
{
// 递归结束条件
if (0 == n)
{
return 0;
}
if (1 == n)
{
return 1;
}
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
int Fib(int n)
{
int n1 = 0;
int n2 = 1;
int num = 0;
int i = 1;
if (0 == n)
{
return 0;
}
if (1 == n)
{
return 1;
}
for(i = 1;i < n;i++)
{
num = n1 + n2;
n1 = n2 ;
n2 = num;
}
return num;
}
int main()
{
int n = 0;
int m = 0;
n = Fibonacci(15);
printf("%d \n",n);
m = Fib(15);
printf("%d \n",m);
return 0;
}
下图为递归实现的计算过程,其中有很多重复步骤。
数字的算法
乘法和除法章节中,假设我们要做乘法13*11,用二进制表示分别为x = 1101 y = 1011,乘法过程:
数字乘法C语言实现:
#include <stdio.h>
int multi(int m,int n)
{
if(1 == n)
{
return m;
}
if(0 == n % 2)
{
return 2*multi(m,n/2);
}
else
{
return m + 2*multi(m,n/2);
}
}
int main()
{
int i = 0;
i =multi(10,15);
printf("%d\n",i);
i =multi(13,11);
printf("%d\n",i);
i =multi(21,15);
printf("%d\n",i);
}
在模的指数运算,C语言递归实现:
#include <stdio.h>
int modexp(int x,int y,int n)
{
if(0 == y)
return 1;
if(y % 2 == 0)
return modexp(x,y/2,n) * modexp(x, y/2, n)%n;
else
return x*modexp(x,y/2,n) * modexp(x, y/2, n)%n;
}
int main()
{
printf("%d \n",modexp(2,10, 3));
return 0;
}
Euclid的最大公因数算法
古希腊数学家Ruclid在2000年前设计了该算法,给定两个整数a和b,该算法将求出能够同时整除两者的最大整数,即通常所说的最大公因数。
最常见的做法是首先对a和b进行因子分解,然后将他们的公共因数相乘。比如1035 =3*3*5*23 ,759 = 3*11*23,所以最大公约数为3*23=69,然而现在没有进行因子分解的有效算法。
Euclid规则:
如果x和y是正整数,且有x>=y,那么gcd(x,y)=gcd(x mod y,y)
用递归实现的终止条件是y==0的时候return x,C语言实现:
#include <stdio.h>
int euclid(int x,int y)
{
if(y ==0) return x;
else
return euclid(y, x%y);
}
int main()
{
printf("%d \n",euclid(96,42));
return 0;
}
分治算法
利用分治算法解决问题通常需要三个步骤:
1.将问题分解为一组子问题,每个子问题都与原问题类型相同,但规模比原问题的规模小。
2.递归求解这些子问题。
3.将子问题的求解结果恰当合并,得到原问题的解。
接着书中列举了几个分治算法应用的例子:
.归并排序
.二分查找
.计算x的n次方
矩阵乘法