书中第一章给提出了一个如下排序问题:
输入:一个至多包含n个非负整数的文件,每个数都小于n; 且这些整数都不重复;数据之间也不存在关联关系。 此处n取值10000000。
约束:①最多1MB的内存空间可用;②磁盘空间充足;③运行时间最多几分钟, 最好是线性时间。
输出:按升序排列的整数序列。
位图排序
针对该题的特点,由于待排序的数据记录较多,如果使用常见的排序方法效率较低,而且内存空间有限(限制为1MB左右),不能一次性将数据如内存,需从文件中多次读入,该书引入了一种新的排序方法 ---位图法。
所谓位图法,就是使用一串二进制串来表示待排序列元素集合的方法。 比如,我们知道一个byte = 8bit,表示成二进制串就是:00000000.我们可以用bit的位置[对于一个字节就是0-7)来表示待序序列中是否出现一个数,1表示出现,0表示不出现。比如说00000010则表示待排序列包含1,因为bit 1为1。
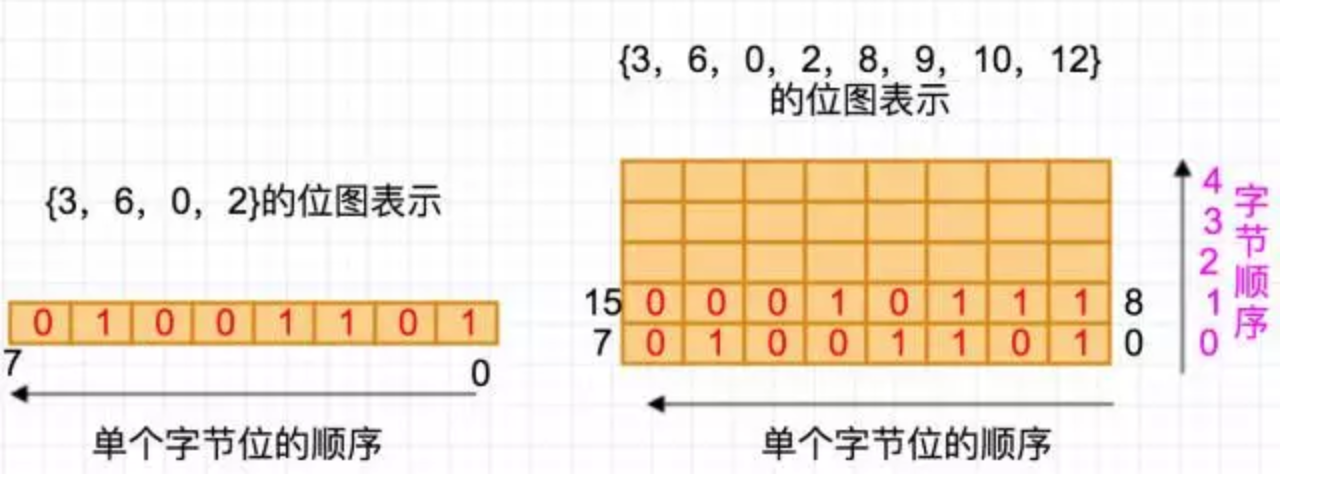
例如:待排序集合{3,6,0,2},由于这个序列的最大数是6,因此用一个byte就够了,因此可以分配一个只含一个元素的char数组,如char arr[1],然后看待排序列第一个元素是3,因此将数组元素的第3bit设为1,依次扫描直到待排序列的最后一个元素2,其位图可以用下图的左边表示。
那么如果待排序列的最大数不能用一个byte的最大位置表示了,比如说{3,6,0,2,8,9,10,12}了。很简单,那么就用2个字节的char数组,char arr[2],比如说待排序列中出现8,那么就将arr数组第二个元素的第0位设为1就可以了,依次类推,如下图右边所示。
好了,现在已经根据待排序列分配好char arr[ ]数组了,也根据待排序列的数据将数组arr的相应位设置好了。最后我们要做的很简单,就是从低到高位依次扫描这个数组的每一位,如果该位为1,表示这个数在待排序列中出现过,那么打印出或者写入到输出文件中,扫描完也就得到了排序后的序列了。
//第一步:将所有的位都置为0;
for i = [0, n)
bit[i] = 0
//第二步:依次读入文件中的每个数,将对应的位都置为1;
for each i in the input file
bit[i] = 1
//检验每一位,如果该位为1,输出对应的整数。
for i = [0, n)
if bit[i] == 1
write i on the output file
借助于C++中的位图,实现代码如下:
#include <bitset>
#include <iostream>
using namespace std;
const int max_element = 12;
int main()
{
int arr[] = {3,6,0,2,8,9,10,12};
bitset<max_element+1> bit;
int size = sizeof(arr)/sizeof(arr[0]);
for(int i = 0;i < size;i++)
{
bit.set(arr[i]);
}
cout<<"After sort: "<<endl;
for(int i=0;i <= max_element;i++)
{
if(bit.test(i))
{
cout<<i<<" ";
}
}
cout << endl;
return 0;
}
输出0 2 3 6 8 9 10 12
如果不借助与C++中的bitset,那么如何实现位向量呢?
#define N 1000000 //表示位向量元素个数
#define BITSPERWORD 32 //int 有32位
#define SHIFT 5 //2^5=32,表示移位
#define MASK 0x1F //二进制11111
int a[1 + N/BITSPERWORD];
#define SET(i){a[i >> SHIFT] |= (1 << (i & MASK));} //第i位 置为1
#define CLR(i){a[i >> SHIFT] &= ~(1 << (i & MASK));} //第i位 置为0
在32位机器中,一个int占4个字节即4*8=32位。
所以在int数组中,a[0]可以表示数字0-31的大小。a[1]可以表示32-63依次类推,在数组中使用1 + N/BITSPERWORD来定义数组大小,是因为需要包含0在内,所以需要+1.
i >> SHIFT表示算数右移5位,即i / 32,该操作的作用是将数组的索引定位到需要操作的那个 int 的位置上,因为我们的位向量结构是由许多个 int 组成的,例如:如果i = 33,i >> SHIFT等于1,首先将第33位定位到了第2个 int 数组中。
i & MASK表示取 i 的最后5位,例:33 & MASK 等于00001,然后把1左移这么多位,即第2位为1,由于前面还有31个
SET操作是取或运算,即把定位到的 int 中的某位设置为1,例:i = 33即把第二个 int 的第2位置1。CLR操作也是同样的道理,只是把对应位置为0。
#include <stdio.h>
#define N 1000000 //表示位向量元素个数
#define BITSPERWORD 32 //int 有32位
#define SHIFT 5 //2^5=32,表示移位
#define MASK 0x1F //二进制11111
int a[1 + N/BITSPERWORD];
#define set(i){a[i >> SHIFT] |= (1 << (i & MASK));} //第i位 置为1
#define clr(i){a[i >> SHIFT] &= ~(1 << (i & MASK));} //第i位 置为0
int test(int i){return a[i >> SHIFT] & (1 << (i & MASK));}
int main()
{
int nums[8]={3,6,0,2,8,9,10,12};
int len = sizeof(nums)/sizeof(int);
for(int i = 0;i < N;i++)
{
clr(i);
}
for(int i = 0;i <len;i++)
{
set(nums[i]);
}
for(int i = 0 ;i < N;i++)
{
if(test(i))
printf("%d ",i);
}
printf("\n");
return 0;
}
输出:0 2 3 6 8 9 10 12