排序就是将一组对象按照某种逻辑顺序重新排列的过程,本文是记录学习排序的总结,持续更新,计划一周时间,视工作忙与否而定。
选择排序
算法思路:
首先找到数组中的最小元素,其次将它和数组的第一个元素交换位置。再次在剩下的元素中找到最小元素,将它与数组的第二个元素交换位置。如此反复,直到将整个数组排序。
算法实现:
#include <stdio.h>
void SelectionSort(int a[],int n)
{
int pos = 0;
int temp = 0;
for(int i = 0;i < n;i++)
{
pos = i;
for(int j = i;j < n;j++)
{
if(a[j] < a[pos])
{
pos = j;
}
}
/*swap a[i]<--->a[pos]*/
temp = a[i];
a[i] = a[pos];
a[pos] = temp;
}
}
/*验证排序后的数组从小到大递增*/
int isSorted(int a[],int n)
{
for(int i = 1;i < n;i++)
{
if(a[i] < a[i-1])
return -1;
}
return 0;
}
int main()
{
int a[10] = {7,8,2,10,9,1,5,4,3,6};
SelectionSort(a, 10);
for(int i = 0;i < 10;i++)
printf("%d ",a[i]);
if(-1 == isSorted(a, 10))
{
printf("Error for selectionSort");
}
return 0;
}
插入排序
通常人们在整理牌的时候是一张一张的来处理,将每一张牌插入到其它已经有序的牌中的适当位置。
与选择排序一样,当前索引左边的所有元素都是有序的,但它们的最终位置不确定,为了给更小的元素腾空间,它们可能会被移动。但当索引到达数组的右端时,数组排序就完成了。
和选择排序不同的一点是,插入排序所需要的时间取决于输入中元素的初始顺序。例如对一个很大且其中的元素已经有序的数组进行排序将会比对随机顺序的数组或是逆序数组进行排序要快的多。
代码部分有个细节要注意的是内层循环的条件j > 0,如果写成j >= 0,在给定的某些情况下不会出错,一旦第二个元素比第一个元素小,且第二个元素为负,那么程序就会报错,例如数组a[10] = {8,-7,2,10,9,1,5,4,3,6}在j >= 0时会出错。
代码实现:
#include <stdio.h>
void InsertionSort(int a[],int n)
{
int temp = 0;
for(int i = 1;i < n;i++)
{
for(int j = i;(j > 0)&&(a[j] < a[j-1]);j--)
{
/*交换两个元素*/
temp = a[j];
a[j] = a[j-1];
a[j-1] = temp;
}
}
}
/*验证排序后的数组从小到大递增*/
int isSorted(int a[],int n)
{
for(int i = 1;i < n;i++)
{
if(a[i] < a[i-1])
return -1;
}
return 0;
}
int main()
{
int a[10] = {7,8,2,10,9,1,5,4,3,6};
InsertionSort(a, 10);
for(int i = 0;i < 10;i++)
printf("%d ",a[i]);
if(-1 == isSorted(a, 10))
{
printf("Error for selectionSort");
}
return 0;
}
上面的代码中存在冗余,满足条件后无需每次交换元素的值,算法导论中第二章关于插入排序的算法,根据伪代码编写为如下代码:
#include <stdio.h>
void insertsort(int a[],int n)
{
int i,key;
for(i = 1;i < n;i++)
{
key = a[i];
while((i>0)&&(key<a[i-1]))
{
a[i] = a[i-1];
i--;
}
a[i] = key;
}
}
int main(int argc, const char * argv[])
{
int a[10]={1,4,8,7,3,2,6,5,10,9};
insertsort(a,10);
for(int i = 0;i < 10;i++)
printf("%d ",a[i]);
return 0;
}
插入排序的另一种形式如下,直接保存当前要插入的元素到temp 中,如果前面的元素值大于当前元素,则使其替换当前元素,然后再对前一个元素作相同操作,如果满足条件依次进行,直到为当前要插入的元素找到正确的位置。这种形式使我们在下面的希尔排序中会用到的形式。
void insert_sort(int arr[],int len)
{
int temp;
int i,j;
for (i = 1; i < len; i++)
{
temp = arr[i];
for(j = i-1; j>=0 && arr[j] > temp ;j -= 1)
{
arr[j+1] = arr[j];
}
arr[j+1] = temp;
}
}希尔排序
对于大规模乱序数组插入排序很慢,因为插入排序只会交换相邻的元素,因此元素只能一点一点地从数组的一端移动到另一端。
例如如果最小的元素正好位于数组的尽头,要将它移动到正确的位置就需要移动N-1次。希尔排序为了加快速度改进了插入排序,交换不相邻的元素以对数组的局部进行排序,并最终用插入排序将局部有序的数组排序。
希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序,算法的最后一步就是普通的插入排序,但是到了这步,需排序的数据几乎是已排好的了(此时插入排序较快)。
假设有一个很小的数据在一个已按升序排好序的数组的末端。如果用复杂度为O(n2)的排序(冒泡排序或插入排序),可能会进行n次的比较和交换才能将该数据移至正确位置。而希尔排序会用较大的步长移动数据,所以小数据只需进行少数比较和交换即可到正确位置。
一个更好理解的希尔排序实现:将数组列在一个表中并对列排序(用插入排序)。重复这过程,不过每次用更长的列来进行。最后整个表就只有一列了。将数组转换至表是为了更好地理解这算法,算法本身仅仅对原数组进行排序(通过增加索引的步长,例如是用i += step_size而不是i++)。
例如,假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ],如果我们以步长为5开始进行排序,我们可以通过将这列表放在有5列的表中来更好地描述算法,这样他们就应该看起来是这样:
13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10
然后我们对每列进行排序:
10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45
将上述四行数字,依序接在一起时我们得到:[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ].这时10已经移至正确位置了,然后再以3为步长进行排序:
10 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45
排序之后变为:
10 14 13
25 23 33
27 25 59
39 65 73
45 94 82
94
最后以1步长进行排序(此时就是简单的插入排序了)。上面的例子来源于维基百科。
代码中的步长采用n/2.并且步长每次/2直到为1。n为数组长度。
#include <stdio.h>
void shell_sort(int arr[], int len)
{
int gap, i, j;
int temp;
for (gap = len >> 1; gap > 0; gap >>= 1)
{
for (i = gap; i < len; i++)
{
temp = arr[i];
for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap)
{
arr[j + gap] = arr[j];
}
arr[j + gap] = temp;
}
}
}
/*验证排序后的数组从小到大递增*/
int isSorted(int a[],int n)
{
for(int i = 1;i < n;i++)
{
if(a[i] < a[i-1])
return -1;
}
return 0;
}
int main()
{
int a[10] = {7,8,2,10,9,1,5,4,3,6};
shell_sort(a, 10);
for(int i = 0;i < 10;i++)
printf("%d ",a[i]);
if(-1 == isSorted(a, 10))
{
printf("Error for selectionSort");
}
return 0;
}
上面代码通过gdb跟踪可以清楚的知道,在gap不等于1的时候,是比较相邻gap元素的大小,使其相对有序,当gap = 1时,退化成插入排序。代码如下:
void insert_sort(int arr[],int len)
{
int temp;
int i,j;
for (i = 1; i < len; i++)
{
temp = arr[i];
for(j = i-1; j>=0 && arr[j] > temp ;j -= 1)
{
arr[j+1] = arr[j];
}
arr[j+1] = temp;
}
}归并排序
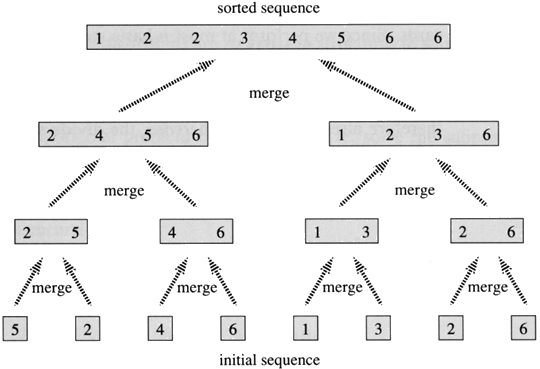
归并排序(Merge Sort,台湾译作:合并排序)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
归并操作(Merge),也叫归并算法,指的是将两个已经排序的序列合并成一个序列的操作。归并排序算法依赖归并操作。归并排序有多路归并排序、两路归并排序 , 可用于内排序,也可以用于外排序。这里仅对内排序的两路归并方法进行讨论。
算法思路:
把 n 个记录看成 n 个长度为 l 的有序子表
进行两两归并使记录关键字有序,得到 n/2 个长度为 2 的有序子表
重复第 2 步直到所有记录归并成一个长度为 n 的有序表为止。
#include <stdio.h>
/*验证排序后的数组从小到大递增*/
void isSorted(int a[],int n)
{
for(int i = 1;i < n;i++)
{
if(a[i] < a[i-1])
printf("Failed.\n");
}
printf("Sucess.\n");
}
void merge_sort_recursive(int arr[], int reg[], int start, int end)
{
if (start >= end)
return;
int len = end - start, mid = (len >> 1) + start;
int start1 = start, end1 = mid;
int start2 = mid + 1, end2 = end;
merge_sort_recursive(arr, reg, start1, end1);
merge_sort_recursive(arr, reg, start2, end2);
int k = start;
while (start1 <= end1 && start2 <= end2)
reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
while (start2 <= end2)
reg[k++] = arr[start2++];
while (start1 <= end1)
reg[k++] = arr[start1++];
for (k = start; k <= end; k++)
arr[k] = reg[k];
}
void merge_sort(int arr[], const int len)
{
int reg[len];
merge_sort_recursive(arr, reg, 0, len - 1);
}
void printarray(int a[],int n)
{
int i;
for(i = 0;i < n;i++)
{
printf("%d ",a[i]);
if((i+1)%10 == 0)
printf("\n");
}
}
int main()
{
int a[20] = {18,7,12,13,2,5,3,4,6,9,8,11,10,15,14,16,20,19,17,1};
merge_sort(a,20);
/*打印数组内容,每10个元素一行*/
printarray(a,20);
isSorted(a,20);
return 0;
}
代码改写成如下方式更加清晰和便于理解:
#include <stdio.h>
/*验证排序后的数组从小到大递增*/
void isSorted(int a[],int n)
{
for(int i = 1;i < n;i++)
{
if(a[i] < a[i-1])
{
printf("Failed.\n");
return;
}
}
printf("Sucess.\n");
}
void merge_arr(int arr[],int start,int mid,int end,int reg[])
{
int start1 = start, end1 = mid;
int start2 = mid + 1, end2 = end;
int k = start;
/*while循环终止条件:两个有序数组中的一个已处理完*/
while (start1 <= end1 && start2 <= end2)
reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
/*1.与下面的while循环同时只有一个成立*/
while (start2 <= end2)
reg[k++] = arr[start2++];
/*1.与上面的while循环同时只有一个成立*/
while (start1 <= end1)
reg[k++] = arr[start1++];
for (k = start; k <= end; k++)
arr[k] = reg[k];
}
void merge_sort_recursive(int arr[], int reg[], int start, int end)
{
if (start >= end)
return;
int len = end - start, mid = (len >> 1) + start;
int start1 = start, end1 = mid;
int start2 = mid + 1, end2 = end;
merge_sort_recursive(arr, reg, start1, end1);
merge_sort_recursive(arr, reg, start2, end2);
merge_arr(arr,start,mid,end,reg);
}
void merge_sort(int arr[], const int len)
{
int reg[len];
merge_sort_recursive(arr, reg, 0, len - 1);
}
void printarray(int a[],int n)
{
int i;
for(i = 0;i < n;i++)
{
printf("%d ",a[i]);
if((i+1)%10 == 0)
printf("\n");
}
}
int main()
{
int a[20] = {18,7,12,13,2,5,3,4,6,9,8,11,10,15,14,16,20,19,17,1};
merge_sort(a,20);
/*打印数组内容,每10个元素一行*/
printarray(a,20);
isSorted(a,20);
return 0;
}
为了便于理解归并排序的执行过程我们可以在程序中添加打印,并重构代码如下:
#include <stdio.h>
void merge_arr(int arr[],int start,int mid,int end,int reg[])
{
int start1 = start, end1 = mid;
int start2 = mid + 1, end2 = end;
printf("Merge %d-->%d\n",start,end);
int k = start;
/*while循环终止条件:两个有序数组中的一个已处理完*/
while (start1 <= end1 && start2 <= end2)
reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
/*1.与下面的while循环同时只有一个成立*/
while (start2 <= end2)
reg[k++] = arr[start2++];
/*1.与上面的while循环同时只有一个成立*/
while (start1 <= end1)
reg[k++] = arr[start1++];
/*拷贝数组内容*/
for (k = start; k <= end; k++)
arr[k] = reg[k];
}
void merge_sort_recursive(int arr[], int start, int end)
{
if (start >= end)
return;
/*len+1是数组长度a[0]……a[len-1]*/
int len = end - start;
int mid = (len >> 1) + start;
/*中间变量,用于合并两个有序数组时*/
int reg[len];
int start1 = start, end1 = mid;
int start2 = mid + 1, end2 = end;
printf("merge_sort a %d %d\n",start,end);
merge_sort_recursive(arr, start1, end1);
merge_sort_recursive(arr, start2, end2);
merge_arr(arr,start,mid,end,reg);
}
int main(int argc, const char * argv[])
{
int a[8]={5,2,4,6,1,3,2,6};
printf("call trace:\n");
merge_sort_recursive(a,0,7);
for(int i = 0;i < 7;i++)
printf("%d ",a[i]);
return 0;
}
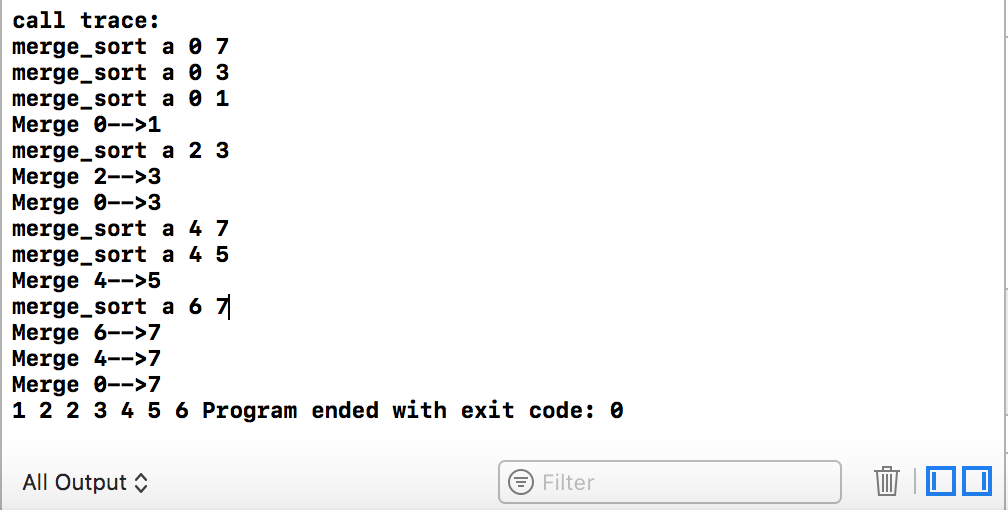
执行结果如下:
打印执行结果与前面介绍归并排序原理时介绍图一致,方便理解递归调用过程。
快速排序
快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略,通常称其为分治法(Divide-and-ConquerMethod)。
分治法的基本思想是:将原问题分解为若干个规模更小但结构与原问题相似的子问题。递归地解这些子问题,然后将这些子问题的解组合为原问题的解。归并排序和快速排序一样均采用了分治法。
C语言实现:
来自算法导论的单向扫描算法,从左往右去扫描直到倒数第二个元素,出现小于最右边的元素则将小的那个元素与i标识的下标的元素交换,单向扫描法存在着冗余的元素交换,比如此时数组已有序1,2,3,4,5,6,单向扫描前5个元素均小于最后的元素6,那么每次都将自己与自己交换。C实现:
#include <stdio.h>
void swap(int *x, int *y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
int Partition(int *arr,int p,int r)
{
int x, i;
x=arr[r];
i=p-1;
for(int j=p; j<=r-1; j++)
{
if(arr[j]<=x)
{
swap(&arr[++i], &arr[j]);
}
}
swap(&arr[++i],&arr[r]);
return i;
}
void QuickSort(int *arr,int p,int r)
{
if(p<r)
{
int q=Partition(arr,p,r);
QuickSort(arr,p,q-1);
QuickSort(arr,q+1,r);
}
}
/*验证排序后的数组从小到大递增*/
int isSorted(int a[],int n)
{
for(int i = 1;i < n;i++)
{
if(a[i] < a[i-1])
return -1;
}
return 0;
}
int main()
{
int a[10] = {7,8,2,10,9,1,5,4,3,6};
QuickSort(a, 0,9);
for(int i = 0;i < 10;i++)
printf("%d ",a[i]);
if(-1 == isSorted(a, 10))
{
printf("Error for selectionSort");
}
return 0;
}
另一种方法是从数组两端进行扫描,左侧扫描到大于"哨兵"的值,右侧扫描出小于"哨兵"的值,然后将两者交换,下面的算法来源于维基百科,仔细读来发现这个快速排序有点意思。我们更常见的形式是以a[left]作为哨兵。
#include <stdio.h>
void swap(int *x, int *y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
void quick_sort_recursive(int arr[], int start, int end)
{
if (start >= end)
return;
int key = arr[end];
int left = start, right = end - 1;
while (left < right)
{
while (arr[left] < key && left < right)
left++;
while (arr[right] >= key && left < right)
right--;
swap(&arr[left], &arr[right]);
}
/*如果arr[left] < key,那么arr[left]将数组分为两部分,否则key将数组分为两部分*/
if (arr[left] >= key)
swap(&arr[left], &arr[end]);
else
left++;
/*上面left++是为了判断类似8 7 6 5 4这种情形,执行到此处时为4 7 6 5 8,此时left为0,无需继续递归排序左半部分*/
if (left)
quick_sort_recursive(arr, start, left - 1);
quick_sort_recursive(arr, left + 1, end);
}
void quick_sort(int arr[], int len)
{
quick_sort_recursive(arr, 0, len - 1);
}
/*验证排序后的数组从小到大递增*/
int isSorted(int a[],int n)
{
for(int i = 1;i < n;i++)
{
if(a[i] < a[i-1])
return -1;
}
return 0;
}
int main()
{
int a[10] = {7,8,2,10,9,1,5,4,3,6};
quick_sort_recursive(a, 0,9);
for(int i = 0;i < 10;i++)
printf("%d ",a[i]);
if(-1 == isSorted(a, 10))
{
printf("Error for selectionSort");
}
return 0;
}